Citra merupakan informasi multimedia dengan jumlah data yang sangat besar di mana kualitasnya sering dikaitkan dengan resolusi citra. Resolusi citra berarti ukuran panjang dan lebar dari sebuah citra dalam satuan pikel. Kedalaman intensitas warna berarti banyaknya bit yang digunakan untuk tiap kode warna yang dinyatakan dalam satuan bit/piksel. Semakin tinggi resolusi citra, semakin banyak jumlah piksel dan kedalaman intensitas warna sehingga mengakibatkan semakin baik kualitas citranya. Tingginya resolusi citra dan kedalaman intensitas warna berarti jumlah bit yang ada semakin banyak sehingga mentransmisikan citra dengan resolusi yang tinggi membutuhkan penyimpanan data citra untuk jumlah bit yang ditransmisikan. Oleh karena itu, untuk meminimalkan jumlah bit yang ditransmisikan, digunakan suatu algoritma kompresi citra.
Kompresi citra dapat dilakukan dalam domain spasial maupun domain frekuensi. Pada kompresi citra dalam domain spasial, redundansi data yang relatif tinggi dalam citra dikodekan dengan menggunakan bit yang lebih kecil. Redundansi berarti banyaknya piksel dari citra memiliki kesamaan secara visual atau kesamaan nilai. Sementara pada kompresi citra dalam domain frekuensi, perlu dilakukan proses transformasi dari domain spasial ke domain frekuensi. Merode transformasi yang digunakan pada penelitian ini yaitu Discrete Cosine Transform (DCT) yang digunakan dalam kompresi JPEG 2000.
Kompresi citra terbagi menjadi dua teknik, yaitu lossy dan loseless. Teknik kompresi citra loseless bekerja dengan membuat kapasitas file dari citra sekecil mungkin yaitu dengan mengoptimalkan teknik pengkodean data redundan yang terdapat pada citra asli. Dalam hal tersebut, kompresi loseless terjadi tanpa ada perubahan data. Salah satu metode yang menerapkan teknik kompresi loseless yaitu metode Huffman. Teknik kompresi citra lossy bekerja dengan mengurangi jumlah bit pada informasi detil citra seperti luminance dan chrominance (warna). Salah satu metode yang menerapkan teknik kompresi lossy yaitu DCT.
Discrete Cosine Transform (DCT)
Metode Discrete Cosine Transform (DCT) mengubah data citra masukan ke dalam format yang dapat mengurangi redundansi piksel. Untuk memetakan nilai piksel ke dalam satu set koefisien, teknik perubahan pengkodean menggunakan reversibel dan linier matematika transformasi. Proses selanjutnya dibutuhkan proses kuantisasi dan pengkodean. Transformasi 2D-DCT dinyatakan dalam persamaan berikut:
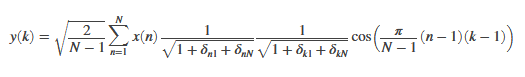
Kuantisasi
Pada tahap kuantisasi, koefisien DCT yang tidak penting dihilangkan guna merekontruksi citra yang baru. Proses kuantisasi menggunakan teknik lossy dengan menyeleksi frekuensi yang tinggi untuk dihilangkan.
Pengkodean Huffman
Prinsip pengkodean Huffman yaitu mengkodekan koefisien hasil proses DCT dengan mengeliminasi nilai-nilai matriks bernilai nol sehingga kelebihan dari keluaran kuantisasi hilang secara zigzag sehingga dihasilkan citra yang sudah terkompresi atau dilakukan kompresi citra.
Program matlab kompresi DCT – Quantization – Huffman
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 | clear allclose allclcI=imread('football.jpg');qy50 = [16 11 10 16 24 40 51 61; 12 12 14 19 26 58 60 55; 14 13 16 24 40 57 69 56; 14 17 22 29 51 87 80 62; 18 22 37 56 68 109 103 77; 24 35 55 64 81 104 113 92; 49 64 78 87 103 121 120 101; 72 92 95 98 112 100 103 99];qc50 = [ 17 18 24 47 99 99 99 99; 18 21 26 66 99 99 99 99; 24 26 56 99 99 99 99 99; 47 66 99 99 99 99 99 99; 99 99 99 99 99 99 99 99; 99 99 99 99 99 99 99 99; 99 99 99 99 99 99 99 99; 99 99 99 99 99 99 99 99;];zz =[1 2 6 7 15 16 28 29; 3 5 8 14 17 27 30 43; 4 9 13 18 26 31 42 44; 10 12 19 25 32 41 45 54; 11 20 24 33 40 46 53 55; 21 23 34 39 47 52 56 61; 22 35 38 48 51 57 60 62; 36 37 49 50 58 59 63 64;];% Konversi Warna Image RGB ke YCbCrIycbcr=rgb2ycbcr(I);[MI,NI,~]=size(Iycbcr);mb=mod(MI,8);nb=mod(NI,8);if nb>0 Iycbcr(:,NI+1:NI+(8-nb),:)=0;endif mb>0 Iycbcr(MI+1:MI+(8-mb),:,:)=0;end[m,n,o] = size(Iycbcr);% Blok CitraImycbcr=Iycbcr;ImDouble = double(Imycbcr);% DCTImDCT = dct(ImDouble);% KuantisasiyDCT = ImDCT(:,:,1);cbDCT = ImDCT(:,:,2);crDCT = ImDCT(:,:,3);y_kuantisasiBlock = @(block_struct) round(block_struct.data ./ qy50) ;c_kuantisasiBlock = @(block_struct) round(block_struct.data ./ qc50) ;y_kuantisasi = blockproc(yDCT ,[8 8] , y_kuantisasiBlock) ;cb_kuantisasi = blockproc(cbDCT ,[8 8] , c_kuantisasiBlock) ;cr_kuantisasi = blockproc(crDCT ,[8 8] , c_kuantisasiBlock) ;% Zig-Zag encodingy_ZigZag = zeros(m*n,1);cb_ZigZag = zeros(m*n,1);cr_ZigZag = zeros(m*n,1);idx = 0;for i=1:8:m for j=1:8:n y_ZigZag(zz+idx) = y_kuantisasi(i:i+7, j:j+7); cb_ZigZag(zz+idx) = cb_kuantisasi(i:i+7, j:j+7); cr_ZigZag(zz+idx) = cr_kuantisasi(i:i+7, j:j+7); idx = idx + (8*8); endendzigZagCoding = [y_ZigZag; cb_ZigZag; cr_ZigZag];% Huffman encodingminDinput=min(zigZagCoding);if minDinput<=0 faktor=minDinput*-1+1;else faktor=0;endzigZagCoding=zigZagCoding+faktor;Hist=zeros(1,max(zigZagCoding));L=length(zigZagCoding);DinputNum=zeros(1,L);for i=1:L DinputNum(i)=zigZagCoding(i); Hist(DinputNum(i))=Hist(DinputNum(i))+1;endPHist=Hist/L;[PHist, symbols]=sort(PHist,'descend');eobi=max(find(PHist~=0));PHist=PHist(1:eobi);symbols=symbols(1:eobi);% Proses Codingdict=huffmandict(symbols,PHist);ImHuffmanEncoder=huffmanenco(zigZagCoding,dict);imKirim = ImHuffmanEncoder;%% ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~imTerima = imKirim;%Huffman decodingImHuffmanDecoder=huffmandeco(imTerima,dict) - faktor;ImDecoder = reshape(ImHuffmanDecoder, m, n, o);y = ImDecoder(:,:,1);cb = ImDecoder(:,:,2);cr = ImDecoder(:,:,3);% Zig-Zag decodingy_DeZigZag = zeros(m,n);cb_DeZigZag = zeros(m,n);cr_DeZigZag = zeros(m,n);idx = 0;for i=1:8:m for j=1:8:n y_DeZigZag(i:i+7, j:j+7) = y(zz+idx); cb_DeZigZag(i:i+7, j:j+7) = cb(zz+idx); cr_DeZigZag(i:i+7, j:j+7) = cr(zz+idx); idx = idx + (8*8); endend% De Kuantisasiy_DekuantisasiBlock = @(block_struct) round(block_struct.data .* qy50) ;c_DekuantisasiBlock = @(block_struct) round(block_struct.data .* qc50) ;y_Dekuantisasi = blockproc(y_DeZigZag ,[8 8] , y_DekuantisasiBlock) ;cb_Dekuantisasi = blockproc(cb_DeZigZag ,[8 8] , c_DekuantisasiBlock) ;cr_Dekuantisasi = blockproc(cr_DeZigZag ,[8 8] , c_DekuantisasiBlock) ;ImDeKuantisasi = cat(3, y_Dekuantisasi, cb_Dekuantisasi, cr_Dekuantisasi);% De DCTImDeDCT = idct(ImDeKuantisasi);ImDeDouble = uint8(ImDeDCT);IDeycbcr = ycbcr2rgb(ImDeDouble);figure('name',['SNR=',num2str(1)]);subplot(1,2,1);imshow(I);title('citra yang dikirim')subplot(1,2,2);imshow(IDeycbcr);title('citra yang diterima') |
hasil kompres-dekompres dengan metode DCT Kuantisasi Zigzag Huffman :
